Introduction
Nowadays, with calculators capable of computing enormous numbers in our pockets, access to websites that allow us to solve complex integrals and derivatives, plot functions, and much more, saying that a board with six lines allows us to do basic arithmetic elegantly and fairly quickly even when using Roman numerals doesn’t necessarily seem impressive. However, boards like this were used for centuries, even for over a millennium, almost all over the world.
The complexity of computing large Roman numerals
Most of us are probably comfortable with adding, subtracting, multiplying, and dividing even larger decimal numbers by hand. Long multiplication and division make this quite intuitive, the grid method and various other algorithms are often taught in school but soon lose relevance as we learn to use a scientific calculator for anything more difficult in higher grades. Computing, especially multiplication and division, has been fairly challenging for larger numbers for most of human history, and anyone who has tried to do these ‘basic’ operations with Roman numerals knows how difficult basic arithmetic can suddenly become.
There are many methods to simplify more complex operations, most of which require only a sheet of paper and a pen, but one that was popular almost everywhere up until the 16th century in Europe was using a Counting Board.
I will go into detail about how we can use a counting board but before that we should first refresh our memory about Roman numerals.
| Roman Numeral | Hindu-Arabic |
|---|---|
| I | 1 |
| V | 5 |
| X | 10 |
| L | 50 |
| C | 100 |
| D | 500 |
| M | 10000 |
The Roman numerals are to the left and the corresponding Hindu-Arabic numbers to the right. To construct a larger number, you combine the letters according to these rules:
Symbols are combined to add their values. For example:
IIis1 + 1 = 2, andVIis5 + 1 = 6.If a smaller number comes before a larger number, you subtract the smaller number from the larger one. For example,
IVis5 - 1 = 4, andIXis10 - 1 = 9.Roman numerals are written from left to right, and the largest value is placed on the left.
A symbol can’t appear more than three times in a row, instead you use rule 3. For example
4is written asIVinstead ofIIII(Some old clocks might use this notation specifically for the number four though).
Simple enough. However, doing basic arithmetic is not necessarily that simple compared to the Hindu-Arabic system - but Roman numerals are all we have now, so what do we do? Exactly, we invent something that allows us to perform arithmetic in an intuitive and simple-to-understand way: The counting board.
A counting board is fairly simple: a board with multiple horizontal lines indicating powers of 10, and the spaces between them indicating five times the value of the line underneath it.

We can place a number on the board by using tokens, coins, stones, or similar items on either the lines or the spaces between them. If we put one on the bottom most line, we add one; if we place two on it, we add two. Placing a token on the space above adds a five. We added three ones and one five, which yields us an eight. We basically build our numeral, which we wrote down on small wax table beforehand (though I suppose no one notices if we use some modern paper for once) as a set of tokens on our table. Note that we only ever added tokens; we do not subtract within one of the three spaces, rather IV is represented as four individual tokens on the line for I - we might have to break some rules here and there for ease-of-use.
Why do we have these three vertical lines dividing the board into three sections (there were examples with only one line or more than three)? Because when we start doing some arithmetic, we need to keep track of the things we are doing. We can have one number in the middle, one to the right, and the result of our operation, including some intermediate values to the left - how someone uses this space is up to the arithmetician.
Now, with an overview of Roman numerals and the ability to put numbers on the table, let’s start doing some actual arithmetic.
Addition
Adding on our setup is fairly straight-forward. We put down one number in the center part and one to the right, then move all the tokens to the left. Simple, really. Although, there is one thing we have to keep in mind. If we want to do 4 + 4, we put down two fours, move them over to get eight tokens on the line for one… Isn’t this a bit difficult to read when we start doing larger numbers? Imagine twelve tokens in one line, eight in the space below, and seven tokens somewhere else. So we add two rules for our table to keep things a bit tidy:
- If we have five tokens on one line we remove them and add one token on the space above.
- If we have two tokens on a space between lines we remove them and add a token on the line above.
This makes sense since VV is not a valid Roman numeral; instead, we use X. Likewise, IIIII is V. Meaning we have to fix our result, remove five of the eight tokens on the line, and place one on the space above. Now we have… VIII. The correct result of IV + IV!
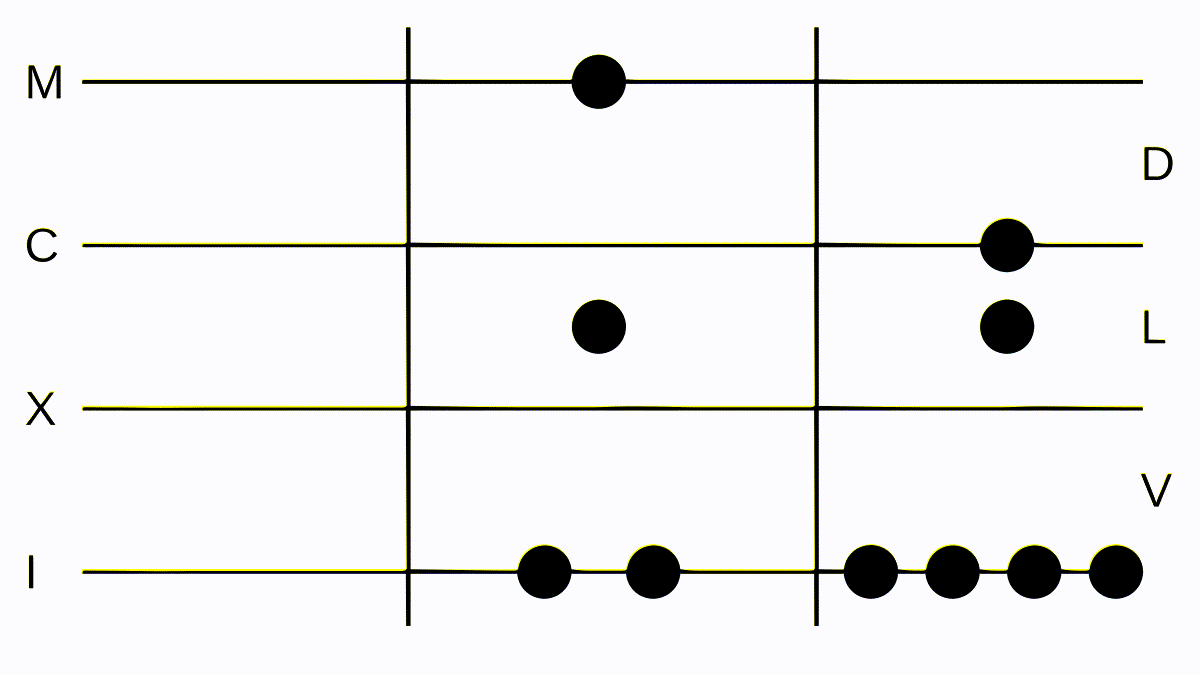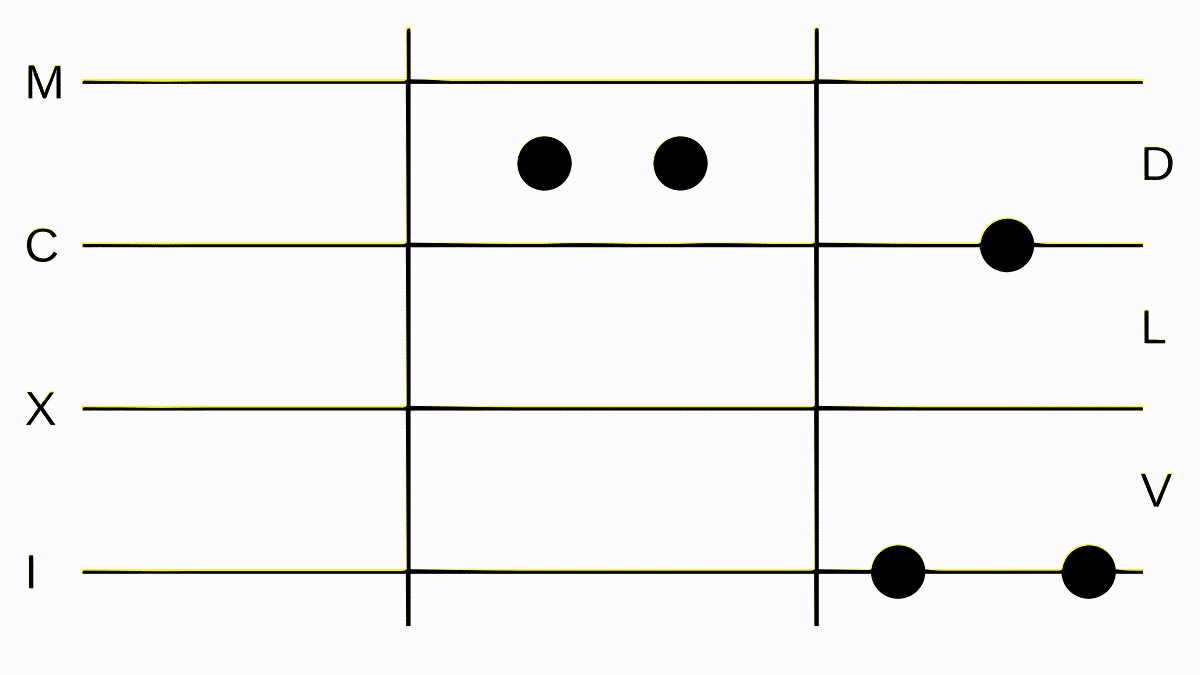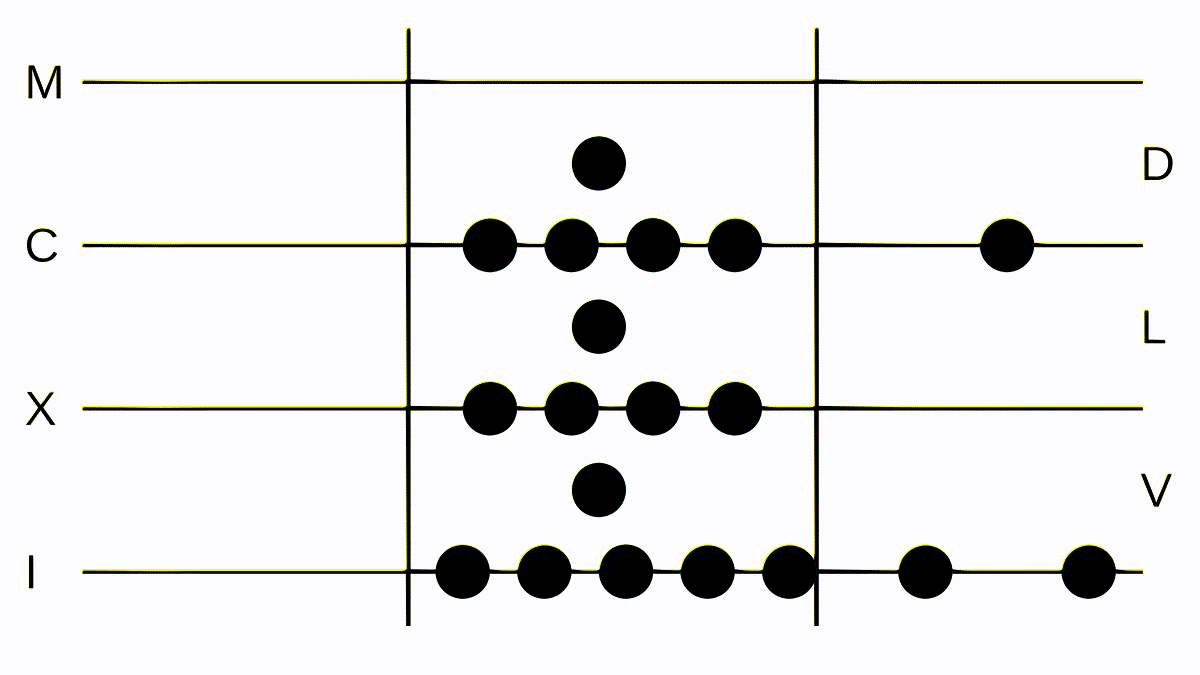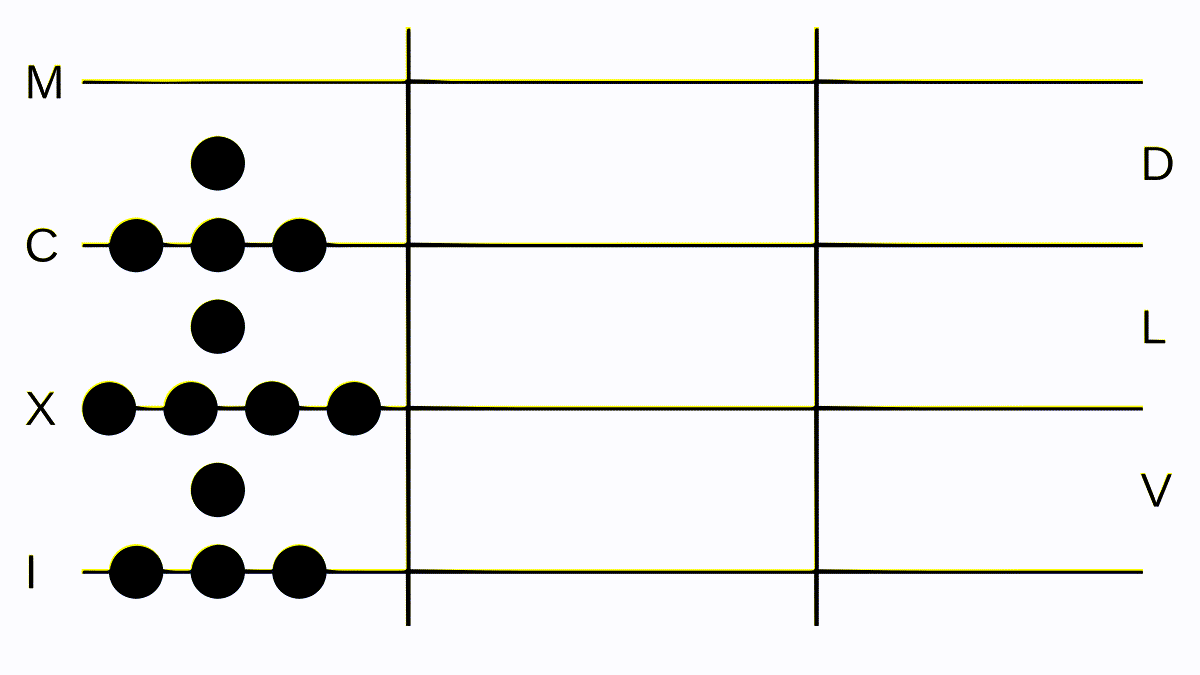
Now let’s add two larger numbers: 152 and 1052. We convert them to Roman numerals: 152 = CLII, which is easy to put down on the board, and 1054 = MLIV or MLIIII on the board. We move all tokens to the left side and get MCLLIIIIII. Let’s clean this up to make it a valid numeral for writing down on our trusty wax tablet, and we get: MCCVI = 1206, which is the correct result.
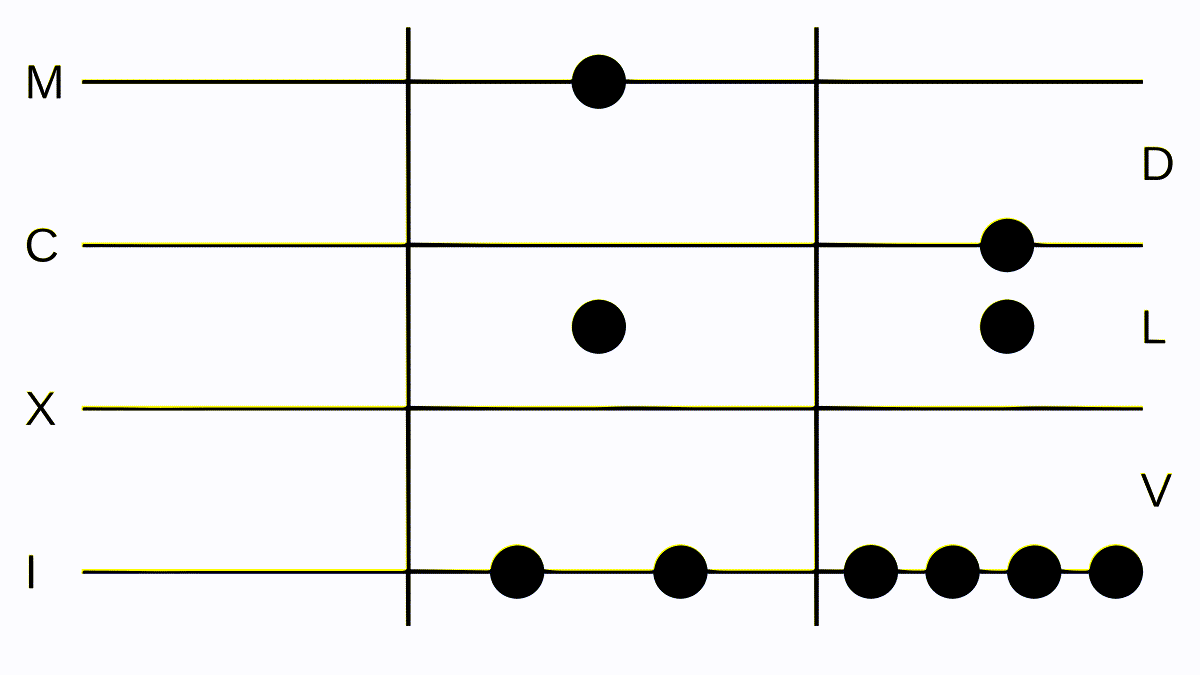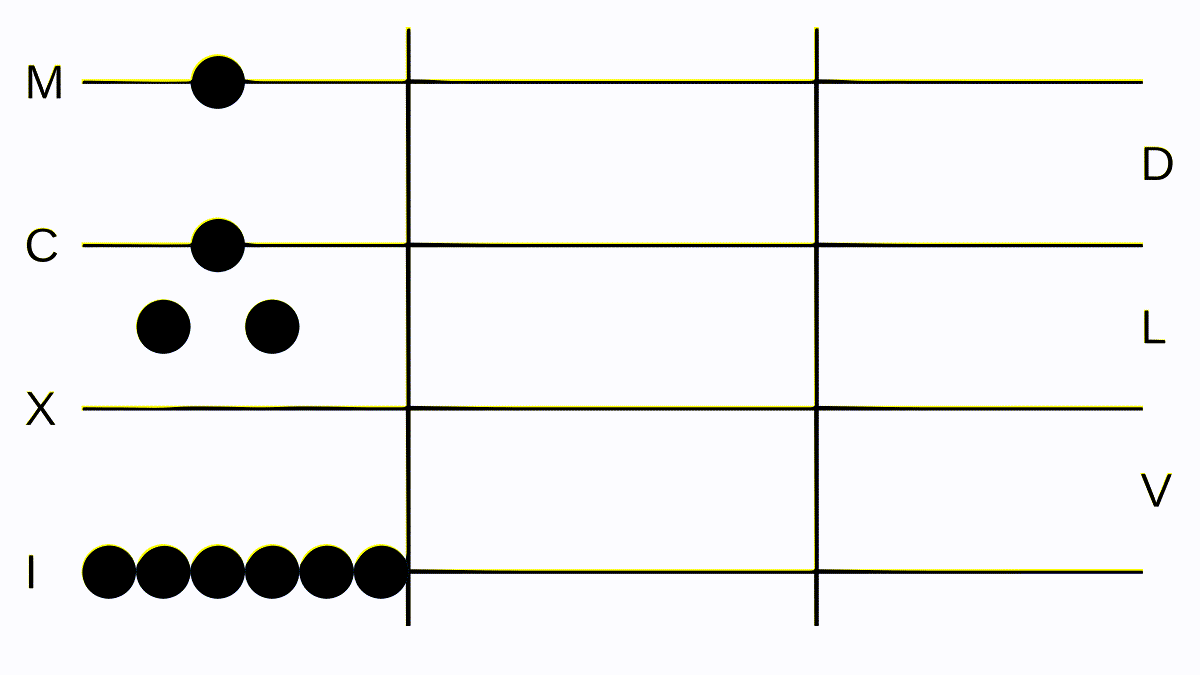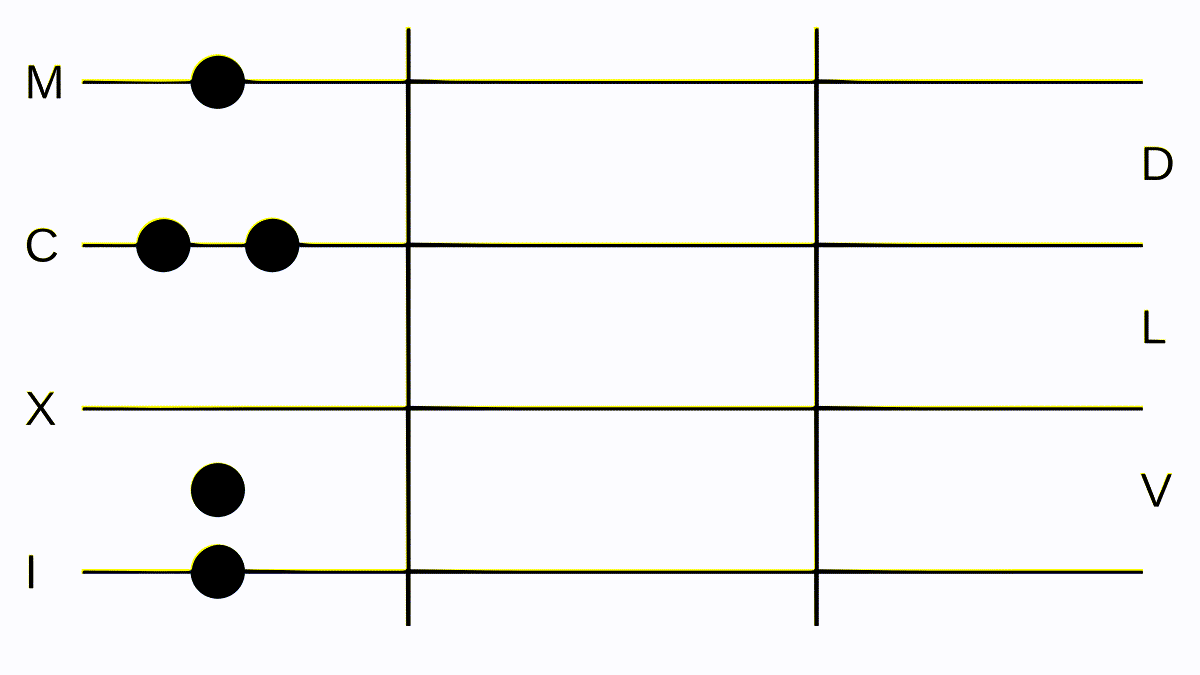
Addition is simple, juts merge the tokens together and correct the result according to the rules
We have taken the first step to becoming a master arithmetician. Next we need to learn another basic skill: subtraction.
Subtraction
Subtracting is actually quite simple too. Place one token on the line for I in one separation and two on the other separation. Now remove one token from each. One separation now has zero tokens, the other only one, because 2 - 1 = 1. We follow this method for subtracting any number from a larger number (Negative numbers? What are those?), and for this we don’t even need the third separation. However we do need one new rule for subtraction:
- If you have a token on a line or space in one separation while not having at least the same amount of tokens on the other separation, you need to convert tokens for larger numbers to lower numbers, breaking the two rules we established for addition.
If we subtract, for example, II from V, we don’t have any tokens on the same line or space in the two separations. We have to convert the V into five I and then apply our operation, removing the same amount of Is on both sides until either has none left, which results in III. This can even be done by simply following patterns; we technically wouldn’t even need to know how to subtract numbers from a theoretical point of view.
But let’s do a more complex subtraction: We subtract CLIV from MLII (by now we are quite capable of placing the tokens on the board, so this part will be skipped). We remove all tokens on both separations on the same line or space until there are none left on one side. We are left with M - CII, so we have to convert our M into some Cs and Is. This has very quickly turned into the most intimidating number we have placed so far on the board: DCCCCLXXXXVIIIII or MCCCLX. But now we can follow our one rule for subtraction again, then convert the result into a valid numeral on our board, which results in DCCCLXXXXVIII or DCCCXCVIII, which is the correct result.
Subtraction, a bit more difficult since we have to shuffle some tokens around but still not that hard
We have learned yet another important arithmetic operation. We know how to add, and we know how to subtract. Multiplication and division are, in principle, for integers, just repeated addition and subtraction. All of the rules we have learned so far will come in quite handy soon.
Multiplication
Multiplication is basically just repeated addition. This is the simplest way of looking at multiplication and it should suffice for our counting board. There are no new rules since we essentially just do addition; we only need to use our board cleverly.
Suppose we wanted to multiply III with II. We lay down the first number in the center, the second one to the right, and start a very simple process: Lay down the same amount of tokens in each space and line as in the middle in the left separation and remove one token from the right separation. Then do that again; now we have no tokens to the right anymore and IIIIII to the left, which we change to VI.
This is how we are going to multiply numbers: add the larger one to the result separation (for us the left one) and remove one I on the right one. This is the same as saying 2 * 3 = 3 + 3. We could also say 2 * 3 = 2 + 2 + 2, but this requires more work and time. If we multiply something with, for example, five, we either convert the five to five Is and do the same as before or come up with some tricks.
If we were to multiply XII with V, we could do first II times V, which we convert to X, and then do V times X, and five tokens on one line are converted to one token on the space above. In fact, multiplying by five is almost trivial in a lot of cases. Multiplying by X is also trivial; we just move the token(s) over the space above to the line above. VII times X is LXX.
I won’t go over all tricks (and there certainly are more than I know), but performing some multiplications and thinking about optimizations, we can very quickly find some neat tricks that make our lives much easier and our calculations significantly faster.
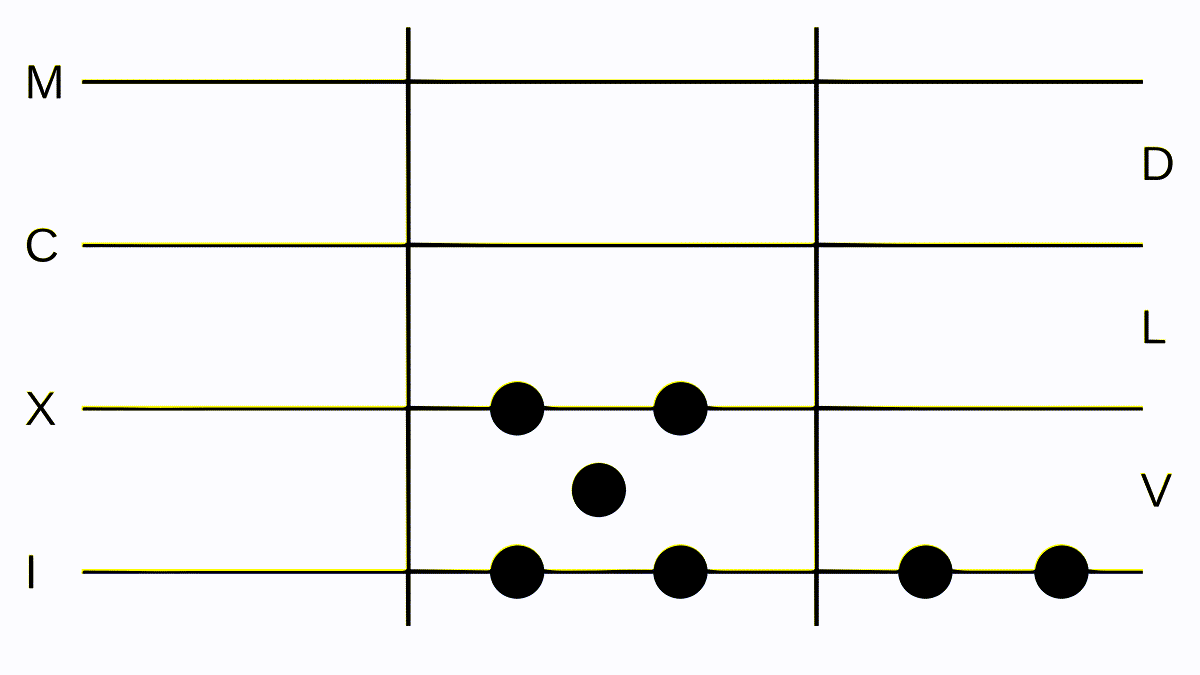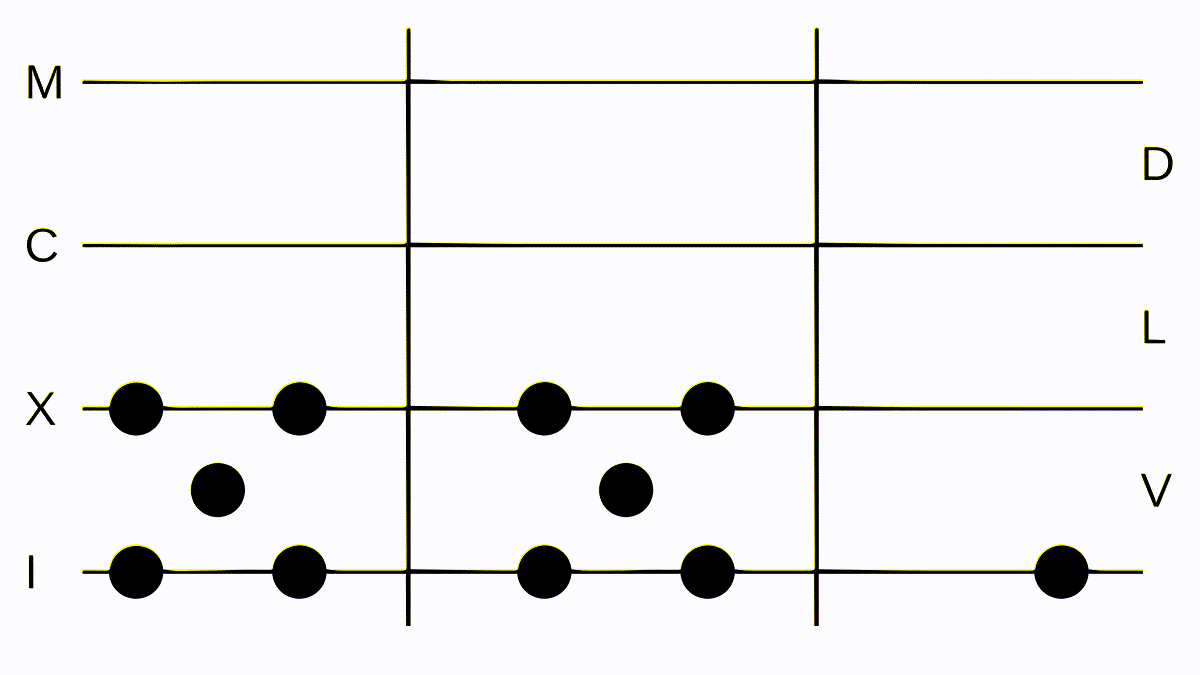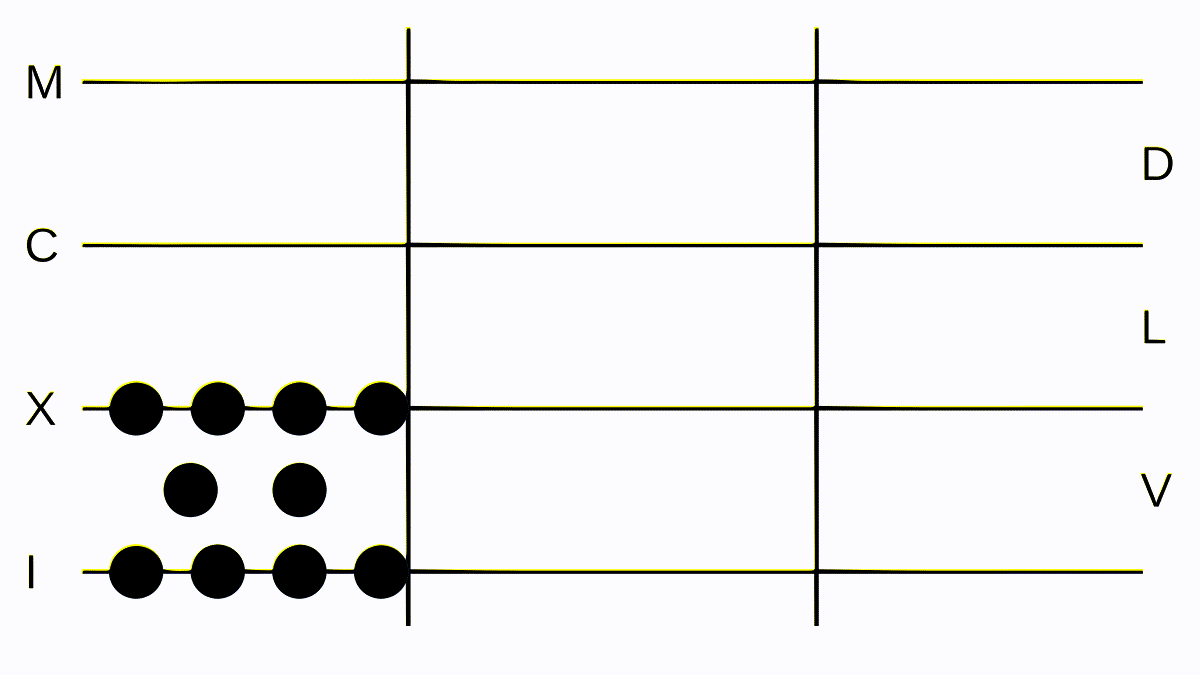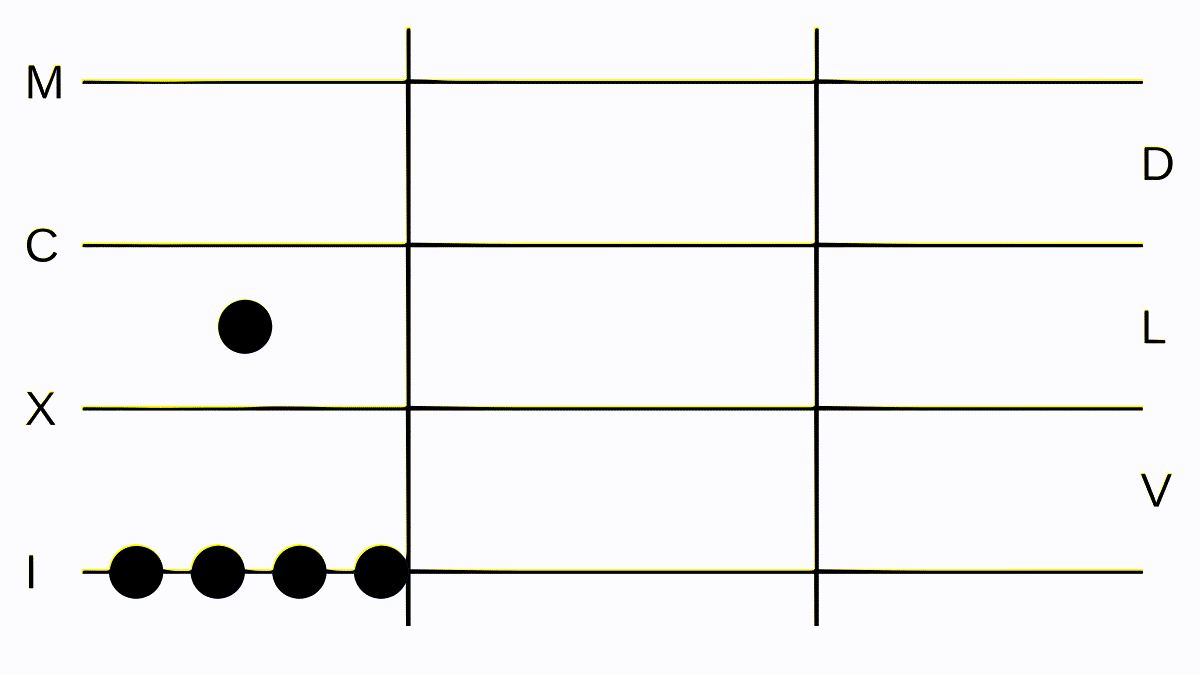
Multiplication, repetitive but intuitive
Division
Let’s face the most difficult operation: division… but first we should refresh some basic math (don’t worry, we’ll do them with Hindu-Arabic numbers) concerning the division of integers.
If we divide 10 by 2, we get 5. Trivial for pretty much anyone, but what did we actually do? You could either say we looked at how often two “goes into” ten, or, and I assume you already know where this is going, we looked at how often we can subtract two from ten until we reach zero. So we could also say 10 ÷ 2 = 5 because 10 - 2 * 5 = 0. This also works with numbers that aren’t properly divisible by adding the remainder.
For example: 13 ÷ 5 = 2 R 3 because 13 = 2 * 5 + 3 or 0 = 13 - 2 * 5 - 3. We use the latter perspective on division for our counting board.
Let’s start by laying down some numbers: XIII in the center and V to the right. We then look whether we can subtract V using our subtraction rules; no we can’t, so we have to convert one X to VV. Now we subtract one token from only the center separation and add one token at the I line to the left. We can do this again until no V-tokens are left in the center. What about the three Is? Well, they are our remainder and we let them lie there.
So our approach is as follows: Larger number in the center, smaller to the right, we apply our subtraction rule with two new rules (sorry I lied earlier):
- Only remove tokens in the center separation
- Only remove tokens when you can remove all tokens that appear on the right separation. So if you have one
Iand oneVto the right you should only ever remove tokens in the center if you can remove oneIand oneVat the same time.
Rule 2 means that if you cannot apply a subtraction at all lines and spaces at the same time, you either convert tokens of larger numbers to more tokens of smaller numbers until you can or you have reached the end of our division.
Let’s look at a more complex example: CCIX divided by LXVII. We lay down our tokens and realize we can’t subtract anything. So we convert one C to one L and five X. Now we can subtract our number on the right from the number in the center exactly once: we lay down one token at I. Again we can’t subtract the whole number on the right, so we convert and propagate our remaining token at the C and start subtracting again. We can subtract our number on the right three times with a remainder of eight - the correct result.
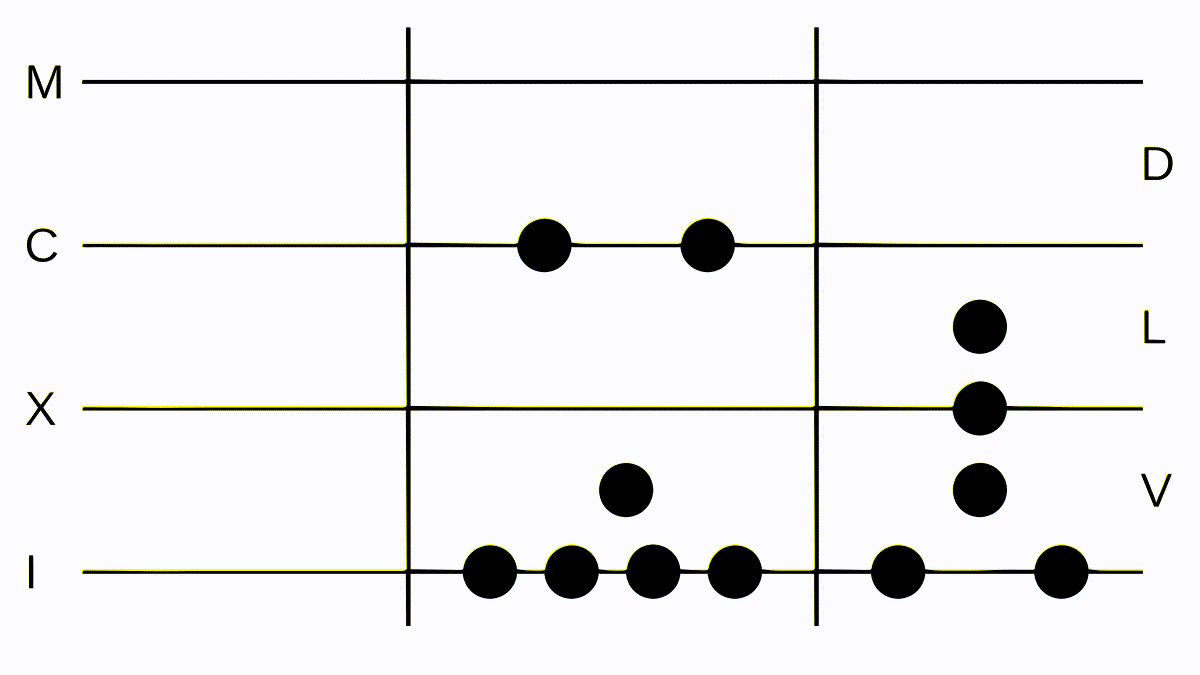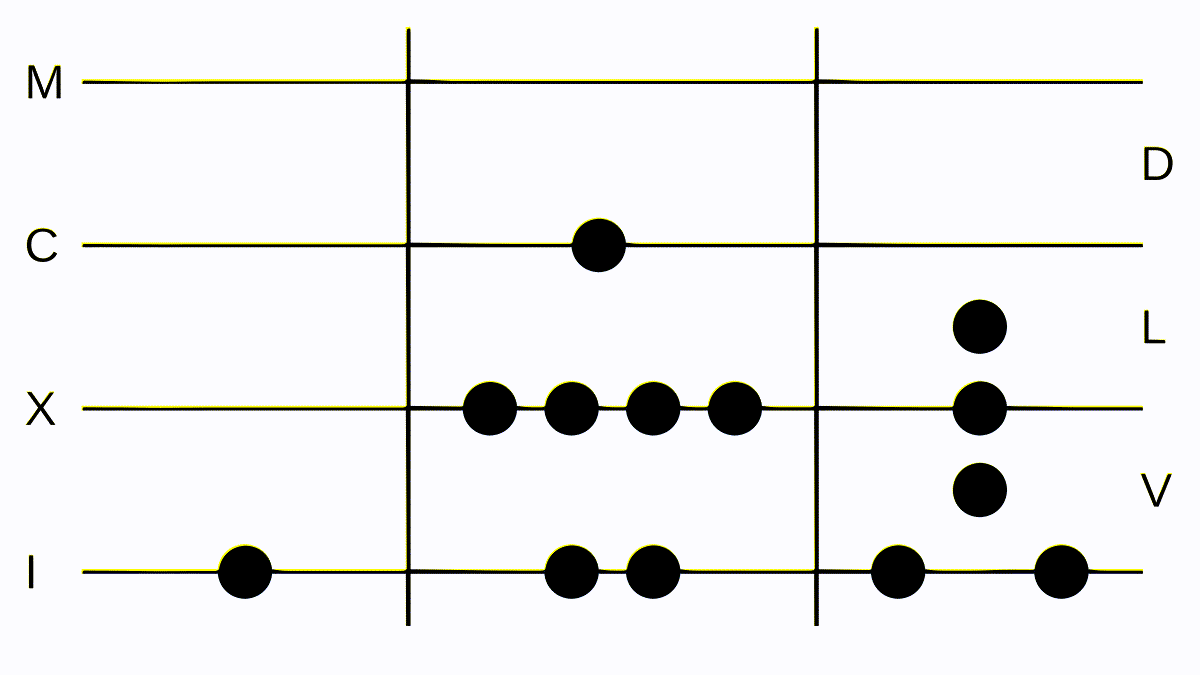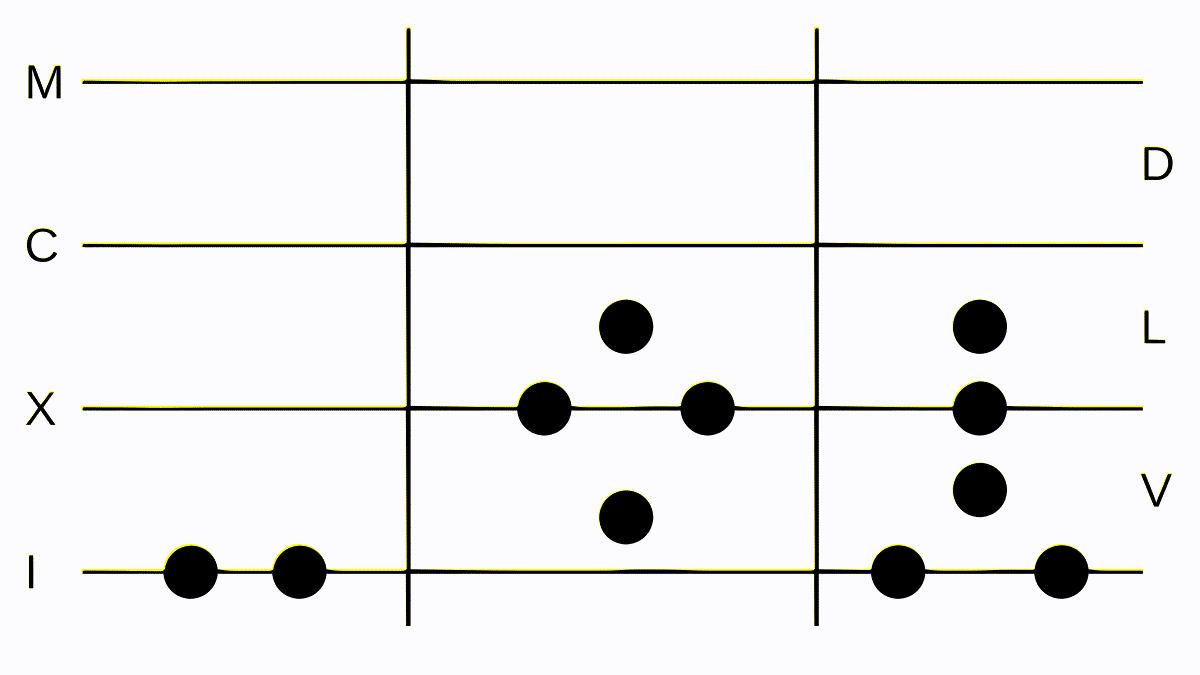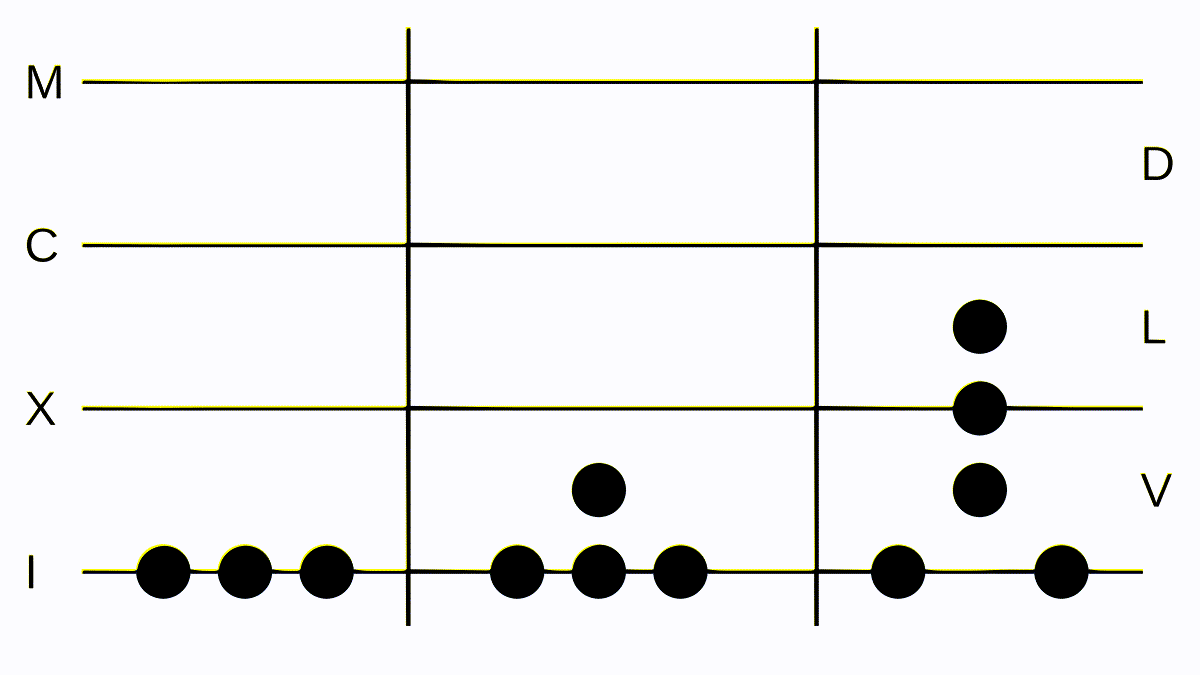
Division, the most laborious of the four arithmetic operations but intuitive, isn't it?
Did you notice something? We searched for the pattern on the right separation among the tokens of the center separation. To make this a bit clearer, let’s divide XXIV by XII (twelve was an incredibly important number in accounting, trade, taxation… pretty much everywhere). If we look at what we have in front of us, we could arrange the tokens in the center separation (XXIIII) as two XII triangles, which we can also do with the tokens to the right. How often does our triangle to the right fit into the shape in the center? Twice, so XXIV divided by XII is II.
Division basically breaks down to searching the pattern in the separation with the smaller number in the separation of the larger number and writing down how often it can appear.
And with this, we have learned all the four basic arithmetic operations - or so we could think. People in the Middle Ages also considered doubling and halving so important that they wrote down rules for those separately. This was very useful because we can abstract some more complex calculations to doubling and halving. (Think of 25 * 13. We double thirteen and multiply by ten, then we could multiply thirteen with ten separately, half that, and add the two results together.)
Why was this used for such a long time?
Counting boards, or ‘computing on lines’ as the German arithmetician Adam Ries called it in his book Rechnung auff linihen, are an intuitive way of learning and understanding basic arithmetic. Some readers might have learned basic mathematics in primary schools with an abacus for exactly the same reason - and an abacus is not much different from a counting board.
Any lay person, anyone who did not spend some time doing calculation after calculation, could observe someone doing this and follow the steps by observing patterns and knowing the most simple of rules. An observer wouldn’t even need to know any mathematics or Roman Numerals at all: as long as the rules among and between the lines and spaces, the rules for the different operations are known, you could check whether the merchant in front of you does their job correctly.
One problem with this can arise very quickly though; what if we accidentally move some tokens? We want to lay one down, pick one up, or move some, and by brushing over the board with our arm, we move some of those that should have stayed in place. This can happen undetected very easily with larger numbers. This was one reason why Italian merchants started to have two people independently doing the same calculations twice, writing down both their results and comparing them. If they both have the same result, they are more likely both correct; if not, they might not know where the error is, but they know that there is one and how large the error might be. If it’s just a tiny error, you could ignore it altogether; if not, you might want to redo all the calculations. And so double-entry accounting/bookkeeping was born.
Some closing thoughts {some-thoughts}
While this is not actually relevant in the modern world, any calculator can handle larger numbers in a fraction of a second without error it is still interesting to learn how computing was done centuries ago with a completely different number system. Hindu-Arabic numbers started to replace Roman Numerals, though merchants obstinately continued using the latter well after Italian scientists and scholars started to adopt the foreign numbers in the 13th century (much to the thanks of Fibonacci, who very quickly used the new, foreign notation), simply because of how transparent a counting board is to the layperson.
In fact, here in this article, we have looked at it from a more simplified perspective. In his book “Rechnung auff linihen,” Adam Ries formalizes the conversion of tokens on the line (linie) to tokens in spaces (spacio) and vice versa as elevatio and resolvatio as follows:
Elevation to a line
Liegen fünff rechenpfennig auff einer Linien so hebe die auff/ leg eine in das spacium darüber…
If there lie five pennies on a line, then lift them up and place one in the space above…
Elevatio to a spacio
Hastu aber zwen pfennig in einem spacio so heb die auff vnd leg einen auff die linie darüber
But if thou hast two pennies in one space, then lift them up and place one on the line above…
Resolvatio to a line from a spacio
Heb ihn auff leg einen in das nechst spacium darunder vund 5 auff die linie vnder dem spacio
Lift it up, place one in the next space below, and five on the line under the space…
Elevatio to a spacio from a line
Ligt aber ein pfennig in einem spacio … so leg dafür 5 pfennig auff die linien darunder
But if one penny lies in one space, then place five pennies on the lines below for it
You can read more in this website though it is in German.
One could spend quite some time mastering the techniques from above, creating their own counting board (you could very much extend it by multiple lines) on paper or on wood, find various tricks and simplifications as an exercise, and maybe gain a more intuitive understanding of numbers and arithmetic on the way. You could use dice sides to represent the number of tokens (instead of using six tokens, you could represent that with the face for six from a six-sided dice or use any larger-sided dice), or different objects to represent a different number of tokens (in fact, in some parts of the world, a nut could have represented A amount of tokens, the seed of a fruit B amount of tokens, and so on).
Negative numbers and fractions can be represented on the board by mirroring the board downwards: if you divide XIII by III, you get IV with a remainder of I, which in decimal is 13 ÷ 3 = 4.333... = 4 + 1/3, so laying down the number you divided by as many times as you have tokens on the remainder separation on the mirrored side allows you to represent fractions. Or you could use it for negative numbers, though you might have to adapt some of the rules.
There are a lot of possibilities to make it more usable for modern arithmetic, but either way, the counting board remains a gimmick, something to play around with and a glimpse into the history of mathematics.
We have not looked at any specific methods of simplifying calculations like the Russian peasant methods for multiplication, which would have been well known during the Middle Ages, merely at the methodology for actually computing something.
I hope I managed to instill some sort of fascination for one of the simple but elegant tools and methods people used before modern computing.